Введение

Метод конечных элементов - это численный метод решения задач инженерной и математической физики. Типичные проблемные области, представляющие интерес в инженерной и математической физике, которые решаются с помощью метода конечных элементов, включают структурный анализ, теплопередачу, поток жидкости, массоперенос и электромагнитный потенциал.

Конечно-элементная постановка задачи приводит к системе одновременных алгебраических уравнений для решения, а не требует решения дифференциальных уравнений. Эти численные методы дают приблизительные значения неизвестных в дискретном числе точек континуума. Следовательно, этот процесс моделирования тела путем разделения его на эквивалентную систему меньших тел или единиц (конечных элементов), соединенных в точках, общих для двух или более элементов (узловых точек или узлов) и / или граничных линий и/или поверхности называется дискретизацией. В методе конечных элементов вместо решения задачи для всего тела за одну операцию мы формулируем уравнения для каждого конечного элемента и объединяем их, чтобы получить решение для всего тела.

Как правило, для решения задачи анализа структурных напряжений инженер стремится определить перемещения и напряжения по всей конструкции, которая находится в равновесии и подвергается приложенным нагрузкам. Для многих конструкций трудно определить распределение деформации с помощью обычных методов, и поэтому обязательно используется метод конечных элементов.

Метод конечных элементов является одним из наиболее распространённых методов решения задач математической физики. Это связано с большой универсальностью метода, сочетающего в себе лучшие качества вариационных и разностных методов.

Цель предлагаемой работы заключается в том, что бы донести до широкой аудитории принцип работы данного метода, его сильные и слабые стороны.

Предполагается решение следующих задач:

1. подробно проанализировать метод конечных элементов/
2. описать математическую часть данного метода.
3. рассмотреть варианты решения задач, возникающих в ходе работы метода;
4. описать основные преимущества и перспективы применения метода.

Порядок практического применения метода конечных элементов

Ниже представлены шаги, цель изложения этих общих шагов состоит в том, чтобы познакомить вас с процедурой, которой обычно следуют при постановке задачи с использованием конечных элементов.

Шаг 1. Дискретизация и выбор типа элементов. Включает в себя разделение тела на эквивалентную систему конечных элементов со связанными узлами и выбор наиболее подходящего типа элемента для наиболее точного моделирования фактического физического поведения. Элементы должны быть сделаны достаточно маленькими, чтобы давать полезные результаты, и в то же время достаточно большими, чтобы уменьшить вычислительные затраты. Дискретизированное тело или сетка часто создаются с помощью программ генерации сетки или программ препроцессора, доступных пользователю. Выбор элементов, используемых при анализе методом конечных элементов, зависит от физического строения корпуса в реальных условиях нагрузки и от того, насколько близким к фактическому поведению аналитик хочет видеть результаты.

Шаг 2. Выбор функции перемещения. Функция определяется внутри элемента с использованием узловых значений элемента. Линейные, квадратичные и кубические многочлены являются часто используемыми функциями, поскольку с ними просто работать в формулировке конечных элементов. Однако можно также использовать тригонометрические ряды. Для двумерного элемента функция смещения является функцией координат в его плоскости (скажем, плоскости x-y) Одна и та же общая функция перемещения может использоваться повторно для каждого элемента. Следовательно, метод конечных элементов - это метод, в котором непрерывная величина, такая как перемещение по всему телу, аппроксимируется дискретной моделью, состоящей из набора кусочно-непрерывных функций, определенных в каждой конечной области или конечном элементе.

Шаг 3. Определение деформации/смещения и напряжения/деформация отношения. Необходимы для получения уравнений для каждого конечного элемента. В случае одномерной деформации, скажем, в направлении x, мы имеем деформацию x, связанную со смещением u посредством

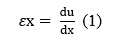
для небольших деформаций.

Кроме того, напряжения должны быть связаны с деформациями с помощью закона напряжений/деформаций, обычно называемого определяющим законом. Способность точно определять поведение материала наиболее важна для получения приемлемых результатов. Простейший из законов напряжения / деформации, закон Гука, который часто используется в анализе напряжений, задается

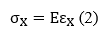
где σ_X = напряжение в направлении x и E модуль упругости.

Шаг 4. Выведение матрицы жесткости элемента и уравнения. Первоначально основывалась на концепции коэффициентов влияния жесткости, которая предполагает опыт структурного анализа. Мы немного затронем альтернативные методы, которые не требуют такой специальной подготовки.

Метод прямого равновесия. В соответствии с этим методом матрица жесткости и уравнения элементов, связывающие узловые усилия с узловыми перемещениями, получаются с использованием условий силового равновесия для базового элемента, наряду с соотношениями сила/деформация.

Методы работы или энергии. Для разработки матрицы жесткости и уравнений для двух и трехмерных элементов гораздо проще применить метод работы или энергии. Принцип виртуальной работы (с использованием виртуальных перемещений), принцип минимальной потенциальной энергии и теорема Кастильяно - это методы, часто используемые с целью вывода уравнений элементов

Принцип виртуальной работы, применим к любому поведению материала, тогда как принцип минимальной потенциальной энергии и теоремы Кастильяно применимы только к эластичным материалам. Кроме того, принцип виртуальной работы может быть использован даже тогда, когда потенциальная функция не существует. Однако все три принципа приводят к идентичным элементным уравнениям для линейно-упругих материалов; таким образом, какой метод использовать для такого рода материалов при структурном анализе, в значительной степени зависит от удобства и личных предпочтений.

Методы взвешенных остатков. Полезны для разработки уравнений элементов; особой популярностью пользуется метод Галеркина. Эти методы дают те же результаты, что и энергетические методы, везде, где энергетические методы применимы. Они особенно полезны, когда такой функционал как потенциальная энергия недоступен. Методы взвешенных остатков позволяют применять метод конечных элементов непосредственно к любому дифференциальному уравнению. Использование таких методов приведет к получению уравнений для описания поведения элемента. Эти уравнения удобно записать в матричном виде в виде

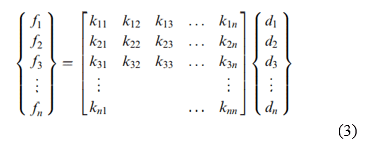
или в компактной матричной форме в виде

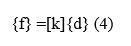
где {f} - вектор узловых сил элемента, [k] - матрица жесткости элемента (обычно квадратная и симметричная), а {d} - вектор неизвестных узловых степеней свободы элемента или обобщенных перемещений, n. Здесь обобщенные перемещения могут включать такие величины, как фактические перемещения, наклоны или даже искривления.

Шаг 5. Сбор уравнения элементов, чтобы получить глобальные или суммарные уравнения и ввести граничные условия. На этом этапе уравнения узлового равновесия отдельных элементов, сгенерированные на шаге 4 , объединяются в глобальные уравнения узлового равновесия. Окончательное собранное или глобальное уравнение, записанное в матричном виде, является

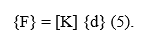
где {F} - вектор глобальных узловых сил, [K] - глобальная матрица структуры или общая матрица жесткости (для большинства задач глобальная матрица жесткости квадратная и симметричная), а {d} теперь является вектором известных и неизвестных узловых степеней свободы структуры или обобщенных перемещений. Можно сказать, что на данном этапе глобальная матрица жесткости [K] является сингулярной матрицей, поскольку ее определитель равен нулю. Чтобы устранить эту проблему сингулярности, мы должны вызвать определенные граничные условия (или ограничения или опоры), чтобы конструкция оставалась на месте, а не перемещалась как твердое тело. На данный момент достаточно отметить, что вызов граничных или вспомогательных условий приводит к модификации глобального уравнения (5). Также необходимо подчеркиваем, что приложенные известные нагрузки были учтены в глобальной матрице сил {F}.

Шаг 6. Решение для неизвестных степени свободы (или Обобщенные перемещения) Уравнение (5), модифицированное для учета граничных условий, представляет собой набор одновременных алгебраических уравнений, которые могут быть записаны в развернутой матричной форме как

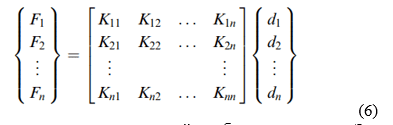
где n - общее число неизвестных узловых степеней свободы структуры. Эти уравнения могут быть решены для ds с помощью метода исключения (такого как Метод Гаусса) или итеративный метод (такой как метод Гаусса–Зайделя). ds называются первичными неизвестными, потому что они являются первыми величинами, определенными с использованием метода конечных элементов жесткости (или смещения).

Шаг 7. Решение для деформаций и напряжений элемента. Для задачи анализа структурных напряжений могут быть получены важные вторичные величины деформации и напряжения (или момента и силы сдвига), поскольку они могут быть непосредственно выражены в терминах перемещений, определенных на шаге 6. Типичные соотношения между деформацией и смещением и между напряжением и деформацией - такие как уравнения (1) и (2) для одномерного напряжения, приведенного на шаге 3, — могут быть использованы.

Шаг 8. Интерпретирование результата. Конечная цель состоит в интерпретации и анализе результатов для использования в процессе проектирования / анализа. Определение мест в конструкции, где возникают большие деформации и напряжения, как правило, важно при принятии проектных/аналитических решений. Компьютерные программы постпроцессора помогают пользователю интерпретировать результаты, отображая их в графической форме.

Преимущества метода

Этот метод обладает рядом преимуществ, которые сделали его очень популярным. Они включают в себя способность:

1. Довольно легко моделировать тела неправильной формы;
2. Справляться с общими условиями нагрузки без затруднений;
3. Моделировать тела, состоящие из нескольких различных материалов, поскольку уравнения элементов оцениваются индивидуально;
4. Обрабатывать неограниченное количество и виды граничных условий;
5. Варьировать размер элементов, чтобы при необходимости можно было использовать небольшие элементы;
6. Изменять модель конечных элементов относительно легко и дешево;
7. Включать динамические эффекты;
8. Справляться с нелинейным поведением, существующим при больших деформациях и нелинейных материалах.

Метод структурного анализа методом конечных элементов позволяет проектировщику выявлять проблемы с напряжением, вибрацией и температурой в процессе проектирования и оценивать изменения в конструкции до создания возможного прототипа. Таким образом, повышается уверенность в приемлемости прототипа. Более того, при правильном использовании этот метод может сократить количество прототипов, которые необходимо построить. Несмотря на то, что метод конечных элементов первоначально использовался для структурного анализа, с тех пор он был адаптирован ко многим другим инженерным и математическим дисциплинам физика, такая как поток жидкости, теплопередача, электромагнитные потенциалы, механика грунта и акустика.

Существует два общих компьютерных метода подхода к решению задач методом конечных элементов. Один из них заключается в использовании крупных коммерческих программ, многие из которых были сконфигурированы для запуска на персональных компьютерах (ПК); эти программы общего назначения предназначены для решения многих типов проблем. Другой заключается в разработке множества небольших программ специального назначения для решения конкретных проблем.

Метод конечных элементов уже реализован во многих системах автоматического проектирования для анализа деформаций, таких как CATIA где над деталью можно проводить эксперименты с разными видами воздействия, на данный момент доступны три вида анализа:

1) Частотный анализ. Для проведения анализа достаточно создать деталь и назначить ей материал, после чего перейти через подпункт меню на экран эксперимента. Необходимо зафиксировать деталь с помощью соответствующего инструмента и указать массу (если необходимо) (см. рис. 1) .

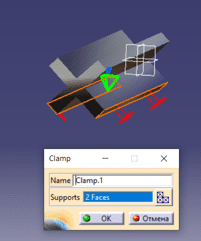
Рисунок 1

После завершения подготовки можем провести вычисления. Для этого необходимо воспользоваться инструментом «Compute», можно так же составить детальный отчет с расчетами с помощью инструмента Analysis Results», где в первой части отчета будут указаны параметры сетки, тип элемента и его качество, расчет материала. Во второй части будет приведен расчет структуры, сдержанности и структурной массы (см. рис. 2).

Рисунок 2

После расчетов формируются три таблицы: Минимальный и максимальный разворот , минимальный разворот, поступательное распределение точек поворота (см. рис. 3).

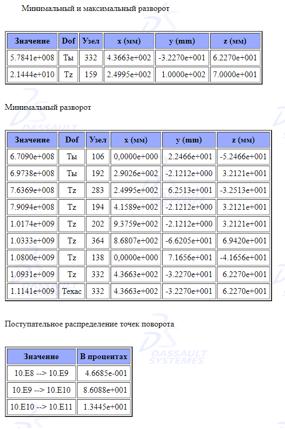
Рисунок 3

Третья часть отчета эта вычисление частоты. Генерируется две таблицы с десятью строками (по числу экспериментов ). Последняя часть отчета показывает, как деталь деформируется во всех 10 сценариях (см. рис. 4). Похожие отчеты будут генерироваться и для других анализов.

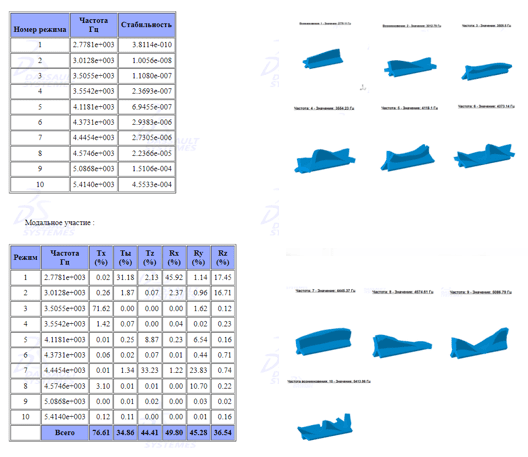
Рисунок 4

После закрытия отчета мы увидим деформированную деталь, полученную при первом эксперименте. CATIA позволяет переключать вид детали, изменив его на отображение сетки, стрессовых зон или деформации по точкам (см. рис. 5).

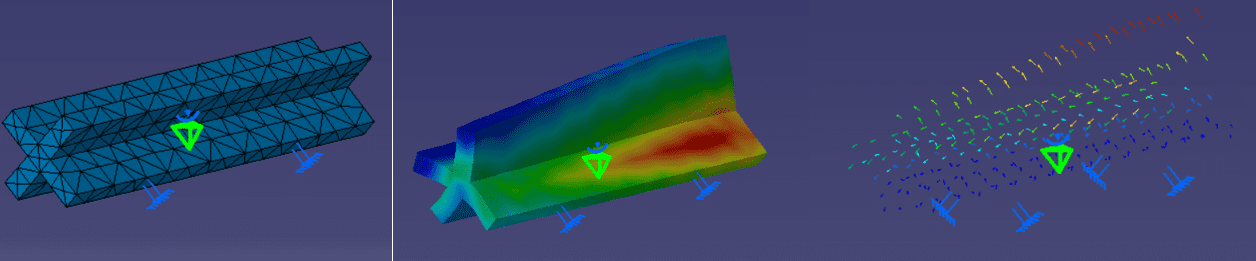
Рисунок 5

Если использовать инструмент «Animate» можно увидеть, как деталь деформируется в режиме реального времени и контролировать анимацию с помощью меню похожего на плеер. При желании можно переключаться через пункты меню и просматривать результаты других экспериментов.

2) Анализ свободной частоты. Главное отличие от обычного частотного анализа состоит в том, что наша деталь находится внутри некоего механизма и движется как бы внутри него, поэтому нам не нужно фиксировать деталь и можно сразу приступить к расчетам. Для этого используем инструмент «Compute» , после генерации отчета воспользуемся меню анимации и получим следующий результат (см. рис. 6).

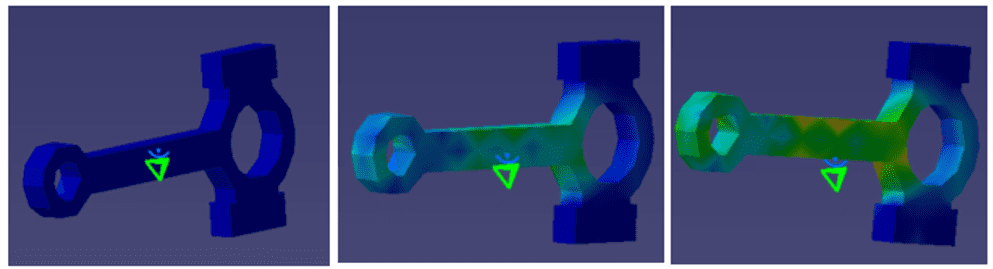
Рисунок 6

На данном рисунке показано движение снизу вверх и стрессовые зоны. Аналогично можно проследить изменения в других экспериментах .

3) Статический анализ. Ис¬поль¬зу¬ет¬ся для оп¬ре¬де¬ле¬ния пе¬ре¬ме¬ще¬ний, на¬пря¬же¬ний, де¬фор¬ма-ций и уси¬лий, воз¬ни¬каю¬щих в кон¬ст¬рук¬ции или ее со¬став¬ных час¬тях при дей¬ст¬вии на¬гру¬зок, не со¬про¬во¬ж-даю¬щих¬ся про¬цес¬са¬ми рас¬сея¬ния энер¬гии или по¬яв¬ле¬ни¬ем су¬ще¬ст¬вен¬ных инер¬ци¬он¬ных эф¬фек¬тов. На данный момент можно оказывать следующие виды воздействий: давление, распределение силы, ускорение, плотность линейной силы, принудительное перемещение, температурное поле, комбинированные нагрузки. Взаимодействие происходит через соответствующее меню (см. рис. 7).

Рисунок 7

Пункт Pressure обеспечивает нормальное давление на поверхность. После нажатия откроется меню, необходимо выбрать поверхности, на которые будет действовать сила и ее значение. Далее нужно воспользоваться инструментом «Compute». В отличие от предыдущих анализов при формировании отчета будет создана таблица прямого метода вычисления, так же изменилась последняя часть с экспериментами, где будет показана деформированная сетка и напряжение Фон Мизеса (узловые значения) (см. рис. 8). Такая часть отчета будет присутствовать и в других видах воздействий.

Рисунок 8

Пункт Distribute Force обеспечивает распределенное давление на поверхность. После выбора команды необходимо выбрать точки приложения силы и значения ее по разным осям , после расчетов можем увидеть результат (см. рис. 9).

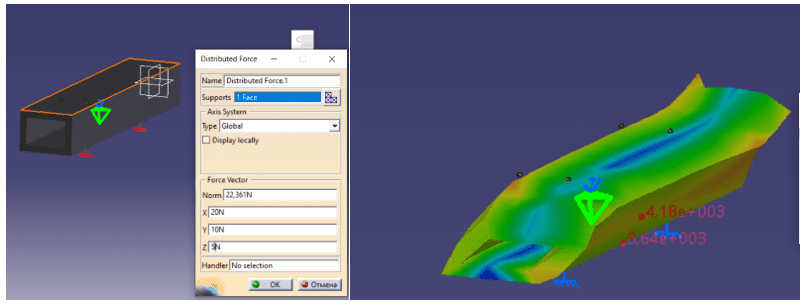
Рисунок 9

Пункт Acceleration позволяет моделировать силы тяжести на деталь. Для использования команды необходимо выбрать деталь, и назначить ускорения свободного падения по различным осям. Будем предполагать что деталь летит вниз без отклонений в горизонтальном положении и установим соответствующие значение . Получим вид деформированной детали после ресчета (см. рис. 10).

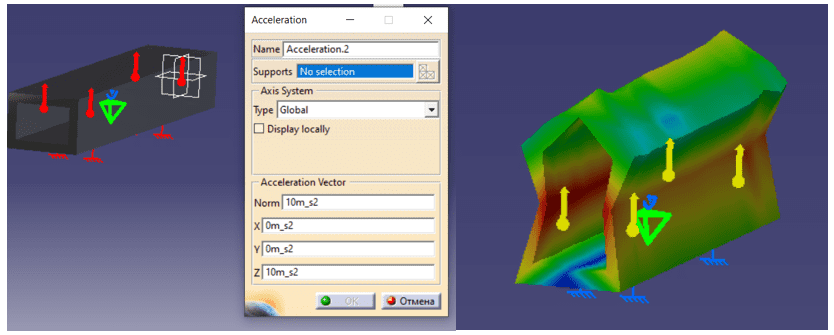
Рисунок 10

Пункт Line Force Density обеспечивает распределенное давление по краям элемента. После выбора команды необходимо выбрать ребра приложения силы и значения ее по разным осям использовать инструмент «Compute» (см.рис.11).

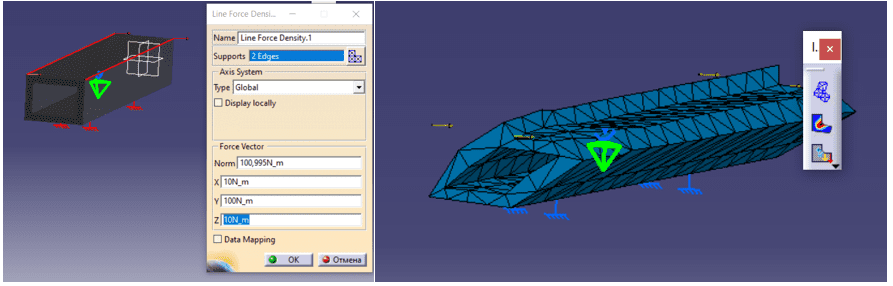
Рисунок 11

Пункт Enforced Displacement показывает, как реагирует деталь в момент удара. После выбора команды необходимо выбрать тиски, которые фиксируют деталь, указать значения и рассчитать. Внешне деталь никак не меняется , показывается только напряжение на участок детали в момент удара (см. рис. 12).

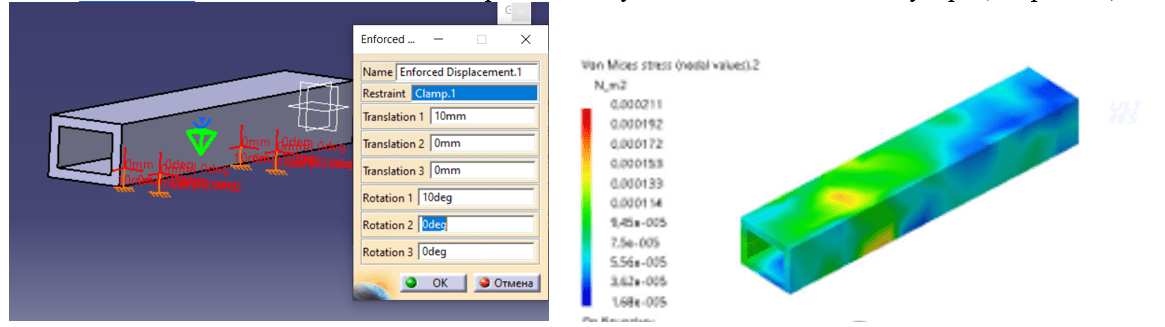
Рисунок 12

Пункт Temperature Field позволяет рассчитать температурные деформации тела . После появления меню настройки необходимо выбрать тело , указать температуру в Кельвинах и использовать инструмент «Compute» , после расчетов получим следующий результат (см. рис. 13).

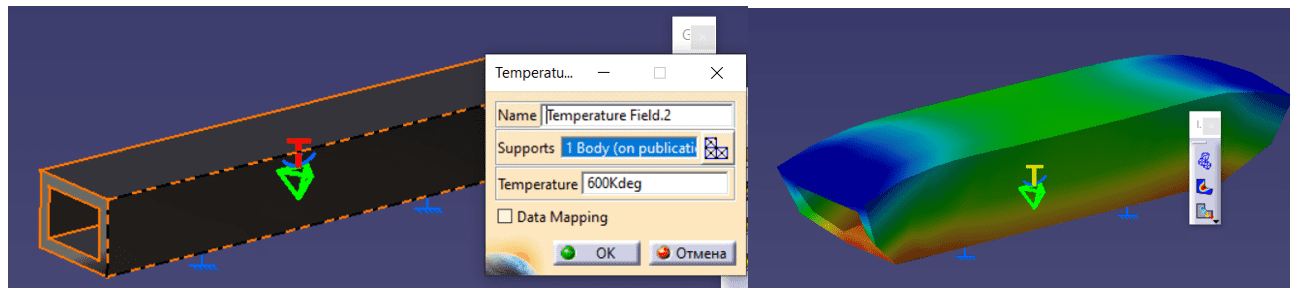
Рисунок 13

Пункт Combined loads. Если необходимо провести эксперимент с несколькими типами воздействий одновременно в CATIA это можно сделать. Для этого на нашу деталь окажем воздействие прессом и давлением применив соответствующие инструменты . Используем инструмент «Compute» , мы можем увидеть, что при деформации учитываются оба воздействия (см. рис. 14).

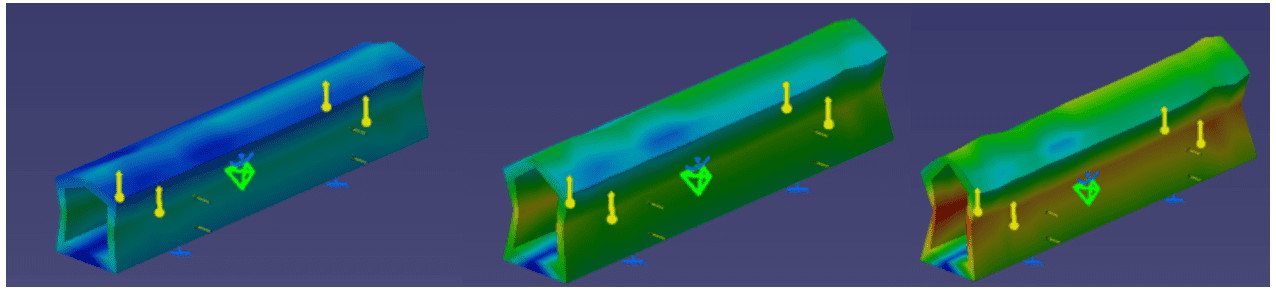
Рисунок 14

Стоит отметить, что метод конечных элементов не ограничен только этими видами анализа. В будущем с развитием ПО станет возможным применения данного метода для любых деформаций элементов с учетом всех условий окружающей среды.

Такие факторов как коррозия, циклические нагрузки, засоры, усталость металла и т.д. станут доступны к изучению непосредственно на стадии проектирования, что позволит снизить затраты на ремонт и расходы связанные с эксплуатацией оборудования, повысить производительность и качество готовых изделий .

Заключение

В настоящее время метод конечных элементов (МКЭ) прочно занимает лидирующее положение в практике инженерных расчетов строительных конструкций, зданий и сооружений, является мощным инструментов при проведении научных исследований.

Огромной популярности метода способствовали следующие преимущества метода: общность подхода при решении различных задач расчета конструкций (в том числе сложных, состоящих из различных конструктивных элементов различной мерности), относительная простота учета взаимодействия конструкции с окружающей средой (механические, температурные, коррозионные воздействия, граничные условия и т.д.), высокая степень приспособляемости к автоматизации всех этапов расчета, естественная механическая трактовка и возможность построения моделей на основе физического, а не математического подхода, возможности рассмотрения неоднородных тел произвольной природы и т.д.

В статье выполнены следующие задачи: изложен метод конечных элементов, подробно описаны варианты решения задач возникающих в ходе работы метода на каждом шаге алгоритма, выделены преимущества применения, выделены основные причины популярности и перспективы развития метода.

Литература

1. Основные формулировки метода конечных элементов в задачах строительной механики. [Электронный ресурс] // КОД - Режим доступа https://cyberleninka.ru/article/n/osnovnye-formulirovki-metoda-konechnyh-elementov-v-zadachah-stroitelnoy-mehaniki-chast-1/viewer
2. Метод конечных элементов [Электронный ресурс] // КОД - Режим доступа https://studfile.net/preview/16408030/page:11/
3. Решение дифференциальных задач методом конечных элементов [Электронный ресурс] // КОД - Режим доступа https://irbis.amursu.ru/DigitalLibrary/AmurSU_Edition/11280.pdf
4. Математика метода конечных элементов [Электронный ресурс] // КОД - Режим доступа https://fea.ru/docs/FEM/Rozin.pdf